前言
回顾第一部分内容,我们学习了线性空间的定义与其的基本性质及线性空间的维度和基。我们了解到线性空间所包含的含义十分广泛,不仅包含线性代数中的向量空间,还包含了函数空间、数列空间等其他的空间。那么,这些不同的线性空间之间又有什么关系与联系呢,我们是否能研究其中某一个线性空间,就能洞悉其他本质相同的空间呢?这一部分我们的主题是线性空间的同构。
在此之前,我们介绍数学中的几个概念。
预备知识
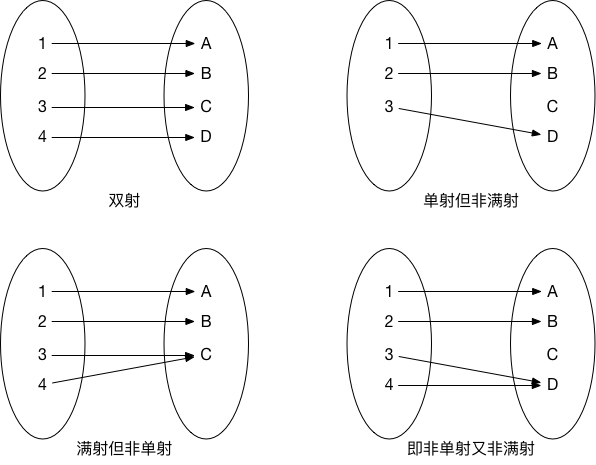
定义 单射 我们称集合$A$到集合$B$的映射$f$为单射,如果对于所有$x,y\in A$,且$x\neq y$,都有$f(x)\neq f(y)$。
定义 满射 一个映射$f:X\to Y$为满射,如果对于任意的陪域$Y$中的元素$y$,在函数的定义域$X$中存在一点$x$使得$f(x)=y$。换句话说,$f$是满射时,它的值域$f(X)$与陪域$Y$相等。
定义 双射 如果一个映射$f:X\to Y$即是单射又是满射,则称$f$为双射。
线性空间的同构
我们现在可以开始定义线性空间的同构了。
定义 同构映射 设$V_1,V_2$是数域$F$上的线性空间,若存在一个$V_1$到$V_2$的双射$\sigma$,使得
- $\forall \boldsymbol\alpha,\boldsymbol\beta\in V_1$,$\sigma(\boldsymbol\alpha+\boldsymbol\beta)=\sigma(\boldsymbol\alpha) + \sigma(\boldsymbol\beta)$
- $\forall k\in F$,$\sigma(k\boldsymbol\alpha)=k\sigma(\boldsymbol\alpha)$
则称$V_1$与$V_2$是同构的,记为$V_1\cong V_2$,这样的映射$\sigma$称为同构映射。
线性空间的同构需要两个空间中的向量一一对应,且满足该映射的线性性质。
同构作为线性空间的一种关系,满足:
- 自反性:对于任意的线性空间$V\cong V$
- 对称性:当$V_1\cong V_2$,有$V_2\cong V_1$
- 传递性:若$V_1\cong V_2$,$V_2\cong V_3$,则$V_1\cong V_3$
本质
由于一一对应的映射保持了线性性,研究线性空间不必要在原有的空间中进行,我们可以通过研究同构的线性空间来描述原有空间。我们期望有一个的线性空间与一大类线性空间同构,这样我们通过这个线性就可以对原有空间进行描述。那么是否存在一个线性空间简洁描述一类空间呢?线性空间本质特征特征又是什么?
定理 设$V$是数域$F$上的$n$维线性空间,则$V\cong F^n$。 证明比较简单,留给大家作为练习。
由以上定理可知,数域$F$上任一$n$维线性空间均与$F^n$同构。故根据同构的传递性,数域$F$上任意两个$n$维线性空间都是同构的。综上所述,我们具有以下定理。
定理 数域$F$上两个有限维线性空间同构的充分必要条件是他们具有相同的维度。
该定理告诉我们,维度是有限维线性空间的唯一本质特征。