数学科学研究问题习惯于将具体地事物分门别类,抽象出各个类别最本质的部分进行讨论。我们弄清楚类别共有性质,我们就可以将这些性质应用于属于这个类别的个例上。今天我们将学习一类集合,在此集合上定义元素间的加法与数乘。如果关于这两类运算封闭(运算结果仍是该集合的元素),那么定义了这两类运算的集合及其中的元素又有什么样的性质呢?这就是我们今天的内容线性空间。
线性空间的定义
在以下表达中,我们将集合的元素称为向量,并讨论在数域$F$上的线性空间,具体地,我们限定讨论的数域是实数域或复数域。我们首先给出线性空间的定义。
定义 我们称非空集合$V$是数域$F$上的线性空间,如果满足:
- (封闭性)对任意向量$\boldsymbol\alpha,\boldsymbol\beta\in V$,有向量和$\boldsymbol\alpha + \boldsymbol\beta\in V$。对于纯量$x\in F$及向量$\boldsymbol\alpha \in V$,有纯量积$x\boldsymbol\alpha\in V$。
- (向量加法运算律)$\boldsymbol\alpha,\boldsymbol\beta\in V$
- $\boldsymbol\alpha+\boldsymbol\beta=\boldsymbol\beta+\boldsymbol\alpha$
- $(\boldsymbol\alpha+\boldsymbol\beta)+\boldsymbol\gamma=\boldsymbol\alpha+(\boldsymbol\beta+\boldsymbol\gamma)$
- 存在零向量 $\boldsymbol0\in V$,使得对任意$\boldsymbol\alpha\in V$,使得$\boldsymbol\alpha + \boldsymbol0=\boldsymbol\alpha$
- 对于每个向量$\boldsymbol\alpha\in V$,存在负向量$-\boldsymbol\alpha$,使得$\boldsymbol\alpha+(-\boldsymbol\alpha)=\boldsymbol0$
- (纯量积运算律)$\boldsymbol\alpha,\boldsymbol\beta\in V$,$x,y\in F$
- $x(y\boldsymbol\alpha)=(xy)\boldsymbol\alpha$
- $1\boldsymbol\alpha=\boldsymbol\alpha$
- $x(\boldsymbol\alpha+\boldsymbol\beta)=x\boldsymbol\alpha+x\boldsymbol\beta$
- $(x+y)\boldsymbol\alpha = x\boldsymbol\alpha+y\boldsymbol\alpha$
线性空间没有规定集合中元素的类型,因此线性空间的概念十分宽泛,包含但并不局限于线性代数中定义的向量空间$\boldsymbol R^n$(n维实向量空间)或$\boldsymbol C^n$(n维复向量空间)。
例 全体收敛的实数数列所组成的集合$l^\infty$是$\boldsymbol R$上的线性空间。其中,对于$\lbrace a_n\rbrace\in l^\infty$和$\lbrace b_n\rbrace\in l^\infty$加法定义为$\lbrace a_n + b_n\rbrace$,$x\in F$,数乘定义为$\lbrace x a_n\rbrace$。
例 定义在闭区间$[0,1]$上的全体连续函数是$\boldsymbol R$上的线性空间。
线性空间是对于定义的向量加法运算与数乘运算而言的。对于定义的运算构成线性空间,但可能对于另一组运算下不构成线性空间。
例 我们规定二维加法运算$(a_1,a_2)+(b_1,b_2)=(a_1+b_1-1,a_2+b_2)$,数乘运算$x(a_1,a_2)=(a_1x,a_2x)$。那么$x[(a_1,a_2)+(b_1,b_2)]=x(a_1+b_1-1,a_2+b_2)=(a_1x+b_1x-x,a_2x+b_2x)$ 而$x(a_1,a_2)+x(b_1,b_2)=(a_1x+b_1x-1,a_2x+b_2x)$。其不满足纯量积的分配律,所以二维向量关于上面定义的加法运算与数乘运算不构成线性空间。
练习 如图阴影所示的集合,在向量加法与数乘运算下是否构成线性空间呢?
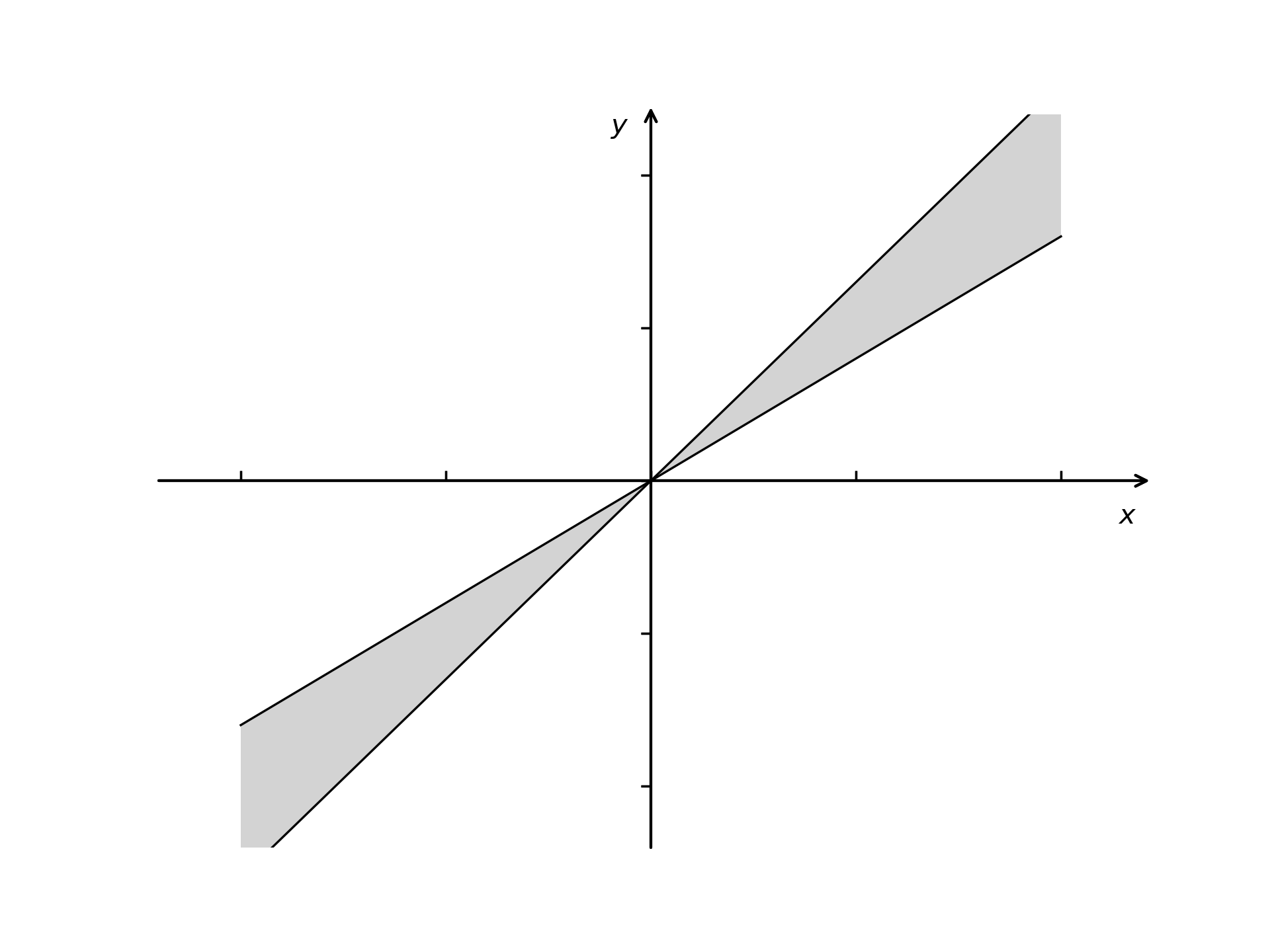
线性空间的性质
略去证明,线性空间具有以下基本性质:
- 性质 1 $0\boldsymbol\alpha=0$,$x\boldsymbol0=0$
- 性质 2 当$x\boldsymbol\alpha=\boldsymbol0$时,有$x=0$或$\boldsymbol\alpha=\boldsymbol0$
- 性质 3 $x(-\boldsymbol\alpha)=-x\boldsymbol\alpha=(-x)\boldsymbol\alpha$
- 性质 4 $(x-y)\boldsymbol\alpha=x\boldsymbol\alpha-y\boldsymbol\alpha$
- 性质 5 $x(\boldsymbol\alpha-\boldsymbol\beta)=x\boldsymbol\alpha-x\boldsymbol\beta$
线性子空间
定义 如果线性空间$V$的子集$U$在线性空间$V$规定的向量加法与纯量积运算下是一个线性空间,称$U$为$V$的线性子空间。
定理 如果$V$是数域$F$上的线性空间,$U$是$V$的非空子集,那么$U$是$V$线性子空间的充分必要条件是该集合满足线性空间的封闭性。即:
对任意向量$\boldsymbol\alpha,\boldsymbol\beta\in U$,有向量和$\boldsymbol\alpha + \boldsymbol\beta\in U$。对于纯量$x\in F$及向量$\boldsymbol\alpha \in U$,有纯量积$x\boldsymbol\alpha\in U$。
线性空间的基与维度
定义 如果线性空间中的任何向量都可以由一组线性无关的向量$\lbrace\boldsymbol\alpha_0,\boldsymbol\alpha_1,…,\boldsymbol\alpha_n\rbrace$线性表示,那么称该组向量为线性空间的基,$n$为线性空间的维度,记为$n=\text{dim} V$。
定理 线性空间中的向量可以由线性空间的基唯一表示。
定理 基的扩张定理 设$\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_r (1\le r \le n)$是$n$维线性空间$V$中$r$个线性无关的向量,则必有$V$中$n-r$个向量$\boldsymbol\alpha_{r+1},\boldsymbol\alpha_{r+2},…,\boldsymbol\alpha_n$存在,使得$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_n\rbrace$成为$V$的基。
证明
- 当$r=n$时,$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_n\rbrace$是$V$的一组基,无需证明。
- 当$r<n$,设$W=Span\lbrace \boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_r\rbrace =\lbrace \boldsymbol\alpha\mid \boldsymbol\alpha=\lambda_1\boldsymbol\alpha_1+\lambda_2\boldsymbol\alpha_2+\cdots+\lambda_3\boldsymbol\alpha_3 \rbrace$。 一定存在$\boldsymbol\alpha_{r+1}\in V$且$\boldsymbol\alpha_{r+1}\notin W$,使得$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_{r+1}\rbrace$线性无关。否则,则不存在$\boldsymbol\alpha_{r+1}\in V$且$\boldsymbol\alpha_{r+1}\notin W$,使得$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_{r+1}\rbrace$线性无关,即对任意$\boldsymbol\alpha_{r+1}\in V$且$\boldsymbol\alpha_{r+1}\notin W$,$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_{r+1}\rbrace$线性相关,即$\boldsymbol\alpha_{r+1}$可以被$\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_r$线性表示,所以$\boldsymbol\alpha_{r+1}\in W$与假设矛盾。按照上述的方式可以将基扩充至$\lbrace\boldsymbol\alpha_1,\boldsymbol\alpha_2,…,\boldsymbol\alpha_n\rbrace$,得证。
线性子空间的运算与维度
定理 设$V_1,V_2$是数域$F$上的线性空间$V$的线性子空间,则$V_1\cap V_2$也是$V$的线性子空间。
定理 设$V_1,V_2$是数域$F$上的线性空间$V$的线性子空间,令$V_1+V_2=\lbrace\boldsymbol\alpha_1+\boldsymbol\alpha_2\mid\boldsymbol\alpha_1\in V_1,\boldsymbol\alpha_2\in V_2\rbrace$,则$V_1+V_2$也是$V$的线性子空间,并称$V_1+V_2$为$V_1,V_2$的和。
需要注意的是
$\boldsymbol\alpha_1+\boldsymbol\alpha_2$可能不属于$V_1,V_2$中任一个空间。例如,$V_1$为二维空间的$x$轴,$V_2$为二维空间的$y$轴,而$V_1+V_2$则覆盖了二维空间的整个平面。
衍生概念 直和 设$V_1,V_2$是数域$F$上的线性空间$V$的线性子空间,若$V_1\cap V_2=\lbrace\boldsymbol0\rbrace$,则称$V_1+V_2$为$V_1$与$V_2$的直和,记作$V_1\oplus V_2$。
定理 $V_1+V_2$是直和的充分必要条件是,对于每个$\boldsymbol\alpha\in V_1+V_2$存在唯一的$\boldsymbol\alpha_1\in V_1,\boldsymbol\alpha_2\in V_2$,使得$\boldsymbol\alpha=\boldsymbol\alpha_1+\boldsymbol\alpha_2$
定理 维度公式 设$V_1,V_2$是数域$F$上线性空间$V$的两个线性子空间,则$\text{dim}(V_1+V_2)=\text{dim}V_1+\text{dim}V_2-\text{dim}(V_1\cap V_2)$。
证明留给大家当个练习吧~
Hint:设$V_1\cap V_2$的基(维度为$m$),然后分别在$V_1$($n$维),$V_2$($r$维)上扩充,共得到$m + (n-m) + (r-m)$个向量,证明$V_1+V_2$中的向量都可以用这些向量线性表示,并证明其线性无关。